What are the Two Kinds?
They are the ‘inclusive or’ and ‘exclusive or’ gates. They both have two inputs and are very similar, but they have a differant output when both inputs are true. The ‘inclusive or‘ gate, or just or gate, as it is the more common, has the following truth table:
As you can see, it is true as long as at least one input is true. This is in contrast to the ‘exclusive or’ gate, or xor gate for short, which is true if only one of its inputs is true, as you can see from the following truth table:
How Do You Make Them?
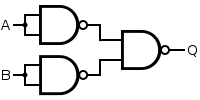
Beginning with the regular or gate, you basically pass the invese of each input through a nand gate, like so:
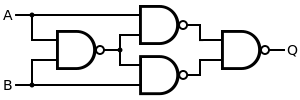
But the xor gate is a bit more complicated and needs four nand gates:
What Can You Use the XOR Gate For?
It is very useful for the foundation of adding numbers together, as will be dicussed next time.
An Alternative Universal Gate
Another universal gate, with which you can make all the other logic gate, is the nor gate, which outputs the inverse of the or gate.
This is how many of either kind of universal gate you need to make the other gates:
As you can see, in general the nand gate is slightly better in this regard, but the real reason it is used, is because they use less transistors.
The Symbols of the Logic Gates:
You might be wondering what the reasons for the differant logic gate symbols are. The basic idea is that the shapes are chosen for each family of gates; OR, AND, and single input. From there, to denote the not variant (like nand and nor) we use a small circle at the end, and to distinguish inclusive and exclusive or gates we use a line at the start.